Cube net problems are a common element of Non-Verbal Reasoning (NVR) tests, especially for Key Stage 2 and 11+ exams. These puzzles challenge students to visualize how 2D shapes fold into 3D cubes. Mastering these types of questions enhances spatial reasoning, logical deduction, and mental visualization—crucial skills for mathematical problem-solving and broader academic performance.
A cube net is a two-dimensional arrangement of six square faces that can be folded into a cube. When folded, each face must align correctly so that opposite faces do not touch and the cube forms without gaps or overlaps. Recognizing valid nets and predicting opposite faces requires practice, observation, and logic.
Each entry describes a unique net pattern and how it folds to form a cube. Opposite face pairings are listed for clarity.
| # | Pattern Name | Shape | Opposite Faces | Simple Explanation |
|---|---|---|---|---|
| 1 | T-Shape | 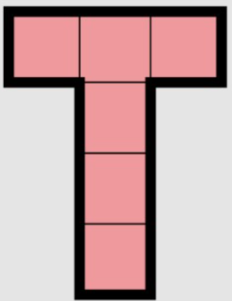 |
(1 ↔ 6), (2 ↔ 5), (3 ↔ 4) | Fold the flaps to make a cube; these faces will be opposite each other. |
| 2 | Plus Sign | 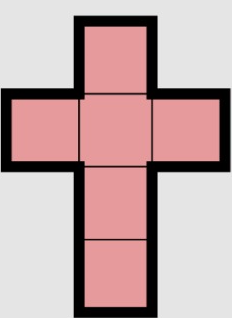 |
(1 ↔ 6), (2 ↔ 4), (3 ↔ 5) | Like a cross that folds into a cube; see which sides touch opposite faces. |
| 3 | T-Rotate Right |  |
(2 ↔ 6), (1 ↔ 5), (3 ↔ 4) | This shape folds so 2 and 6 face each other, and so on. |
| 4 | T-Rotate Left |  |
(1 ↔ 6), (2 ↔ 5), (3 ↔ 4) | Similar to #3 but rotated; faces line up differently. |
| 5 | L with Hat |  |
(1 ↔ 6), (2 ↔ 5), (3 ↔ 4) | Looks like a little hat on L; these pairs will be opposite. |
| 6 | Step Shape |  |
(1 ↔ 6), (2 ↔ 5), (3 ↔ 4) | Like stairs folding up into a cube, with those opposite pairs. |
| 7 | Folded S |  |
(1 ↔ 6), (2 ↔ 5), (3 ↔ 4) | S shape folds so these faces are opposite each other. |
| 8 | Snake |  |
(1 ↔ 6), (2 ↔ 5), (3 ↔ 4) | Like a snake curling up to make a cube. |
| 9 | Corner Cross |  |
(1 ↔ 6), (2 ↔ 4), (3 ↔ 5) | Cross shape with a corner, folding so these faces oppose. |
| 10 | Staircase | 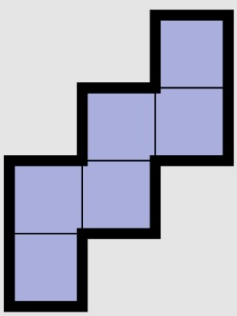 |
(1 ↔ 6), (2 ↔ 5), (3 ↔ 4) | Steps going up, these pairs will be opposite on the cube. |
| 11 | Vertical S | 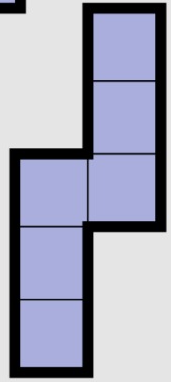 |
(1 ↔ 6), (2 ↔ 5), (3 ↔ 4) | S shape turned vertical, these faces oppose each other. |
Now that you have a solid understanding of cube nets and how they work in Non-Verbal Reasoning questions, here are some suggested next steps:
Cube net questions are not just visual challenges; they build foundational skills in geometry, problem-solving, and abstract thinking. By familiarizing yourself with common patterns and practicing how faces align, students can confidently approach these tasks in NVR exams. Visual aids, physical models, and repeated exposure are excellent tools to deepen understanding and accuracy.